Firstly, we will calculate the z-score for each value => 54.25 and 55.95 inches.
The formula to calculate the z-score will be
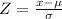
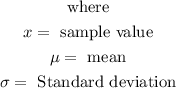
For x = 54.25, the z-score will be
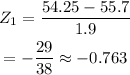
For x = 55.95, the z-score will be
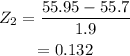
The probability is the shaded portion of the image above.
Therefore,

Therefore, the probability is 0.330 in 3 d.p.