Question

How many different values of a satisfy this inequality 3/16<5/a<7/15

Answer 1

An infinite number of values for 'a' satisfy the inequality 3/16 < 5/a < 7/15, as 'a' can be any number greater than 10.7143 and less than 26.6667.

Step-by-step explanation:

The student is asking how many different values of a satisfy the inequality 3/16 < 5/a < 7/15. We can solve this inequality by first finding the range of values for which a makes the inequality true. To do this, we should first isolate a in the middle of the inequality.

To solve for a, we take the reciprocal of each part of the inequality since a is in the denominator on the middle term. This will reverse the inequality signs:

• Reciprocal of 3/16 is 16/3
• Reciprocal of 5/a is a/5
• Reciprocal of 7/15 is 15/7

The reversed inequality is:

16/3 > a/5 > 15/7

Multiplying each part by 5 to isolate a we get:

80/3 > a > 75/7.

Now, we should find the decimal equivalent of these bounds:

• 80/3 is approximately 26.6667
• 75/7 is approximately 10.7143

Therefore, the value of a can be any number greater than 10.7143 and less than 26.6667. So there is an infinite number of values that a can take to satisfy the inequality.

Answer 2

We are given the following inequality

`(3)/(16)<(5)/(a)<(7)/(15)`

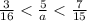
Let us solve the inequality for a.

Flip the fractions (the signs will be reversed)

`(16)/(3)>(a)/(5)>(15)/(7)`

Multiply the inequality by 5

`\begin{gathered} (5\cdot16)/(3)>(5\cdot a)/(5)>(5\cdot15)/(7) \\ (80)/(3)>a>(75)/(7) \end{gathered}`

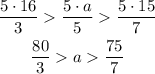
So a must be greater than 75/7 (that is 10.71) next integer is 11 (rounding up)

a must be less than 80/3 (that is 26.67) previous integer is 26 (rounding down)

So, the values of a that satisfy the inequality are

11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26

These are a total of 16 values

Therefore, 16 different values of a satisfy this inequality.