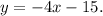I need help finding the equation for a tangent line

Question

asked May 2, 2023 145k views

1 Answer

Sacha Barber · Answer 1 · 2023-05-07T04:50:21+0000

To answer this question we will use the following slope-point formula for the equation of a line:

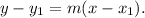
$y-y_1=m(x-x_1)\text{.}$

Recall that f'(x) is the slope of the tangent line to the graph at (x,f(x)).

Therefore, the tangent line of y=f(x) at x=2 has a slope of -4 and passes through (-2,-7).

Then, using the slope-point formula for the equation of a line we get:

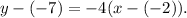
$y-(-7)=-4(x-(-2))\text{.}$

Simplifying the above result we get:

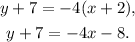
$\begin{gathered} y+7=-4(x+2), \\ y+7=-4x-8. \end{gathered}$

Subtracting 7 from the above equation we get:

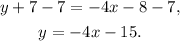
$\begin{gathered} y+7-7=-4x-8-7, \\ y=-4x-15. \end{gathered}$

Answer: