Question

Find the x-intercepts of the parabola with vertex (-5,13) and y intercept (0, -12). Write your answer in this form: (X1,y1),(x2,y2). If necessary, round to the nearest hundredth.

Answer 1

(-1.39, 0) and (-8.61, 0)

Step-by-step explanation:

To find the x-intercepts of a parabola, we need to find the equation of the parabola.

So, the equation of a parabola is:

`y=a(x-h)^2+k`

Where (h, k) is the vertex and a is a constant. Then, replacing (h, k) by (-5, 13), we get:

`\begin{gathered} y=a(x-(-5))^2+13 \\ y=a(x+5)^2+13 \end{gathered}`

Now, to know the value of a, we need to replace (x, y) by the intercept (0, -12) and solve for a, so:

`\begin{gathered} -12=a(0+5)^2+13 \\ -12=5^2a+13 \\ -12-13=25a+13-13 \\ -25=25a \\ (-25)/(25)=(25a)/(25) \\ -1=a \end{gathered}`

So, the equation of the parabola with vertex (-5, 13) and y-intercept (0, 12) is:

`y=-1(x+5)^2+13`

Now, the x-intercepts are the values of x, when y is equal to 0, so we need to solve the following equation:

`-(x+5)^2+13=0`

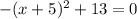
Then, we get:

`\begin{gathered} -(x^2+10x+25)+13=0 \\ -x^2-10x-25+13=0 \\ -x^2-10x-12=0 \\ x^2+10x_{}+12=0 \end{gathered}`

So, to solve the equation, we can use the following equation:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where a is the number besides x², b is the number beside the x and c is the constant.

Therefore, the solutions of the equation are:

`\begin{gathered} x=\frac{-10+\sqrt[]{10^2-4(1)(12)}}{2(1)}=-5+\sqrt[]{13}=-1.39 \\ x=\frac{-10+\sqrt[]{10^2-4(1)(12)}}{2(1)}=-5-\sqrt[]{13}=-8.61 \end{gathered}`

Therefore, the x-intercepts of the parabola are the points (-1.39, 0) and (-8.61, 0)