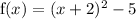Question

Find the vertex form f(x)=x2+4x-1

Answer 1

The vertex form of the equation of a parabola is,

`f(x)=a(x-h)^2+k\ldots\ldots.(1)`

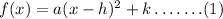
where (h, k) are the corrdinates of the vertex.

The given equation is,

`f(x)=x^2+4x-1\ldots\ldots(2)`

The coefficient of x term is 4.

Add or subtract ((1/2)coeffiicent of x term)^2 from the above equation.

`((1)/(2)*4)^2=4`

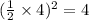
Adding and subtracting 4 from equ (2),

`\begin{gathered} f(x)=x^2+4x-1+4-4 \\ f(x)=x^2+4x+4-1-4 \\ f(x)=(x^2+4x+4)-5 \\ f(x)=(x+2)^2-5 \end{gathered}`
`\text{The equation f}(x)=(x+2)^2-5\text{ is in the form }f(x)=a(x-h)^2+k\text{.}`

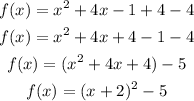
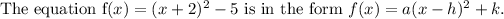
Therefore, the vertex form of the given equation is,

`\text{f}(x)=(x+2)^2-5`