Question

A stone is thrown into a pod, creating a circular ripple that spreads over the pond in such a way that the radius is increasing at a rate of 3.6 ft/sec. Find a function A(r) for the area of the ripple in terms of the radius r.

Answer 1

In general, the area of a circle is given by the formula below

`A=r^2\pi`

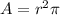
In our case, the radius changes as time passes.

Therefore,

`A(r)=r^2\pi`

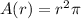
Then, A(r)=pi*r^2.

However, one can obtain a function A(t) by defining r=3.6t, where r is in ft and t is in seconds; thus,

`\Rightarrow A(t)=(3.6t)^2\pi`

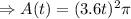
The answer is A(r)=pi*r^2, being r a function of time.