A sinusoidal function is as a sine function. To write our sine function we need to understand its coefficients.
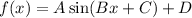
A represents the amplitude, B represents the frequency, C represents the phase, and D represents the vertical translation(in a certain way, can be seen as the mean of the function).
The sine function oscillates between 1 and - 1, therefore, the maximum and minimum value it reaches are
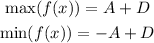
From the text, we know that the maximum number of hours of daylight happens during June, and it is equal to 14 hours, while the minimum number of hours of daylight happens during December and it is 10 hours.
Using this information and the previous equation for maximum and minimum values, we have the following equations

If we add those equation together, we get a new one only for D.
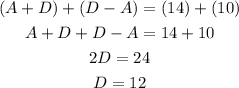
Using this value for D in any of previous equations let us find the amplitude value.

From this, we already know the amplitude and vertical translation of our function.
To determinate the period of our function, we're going to use the information that the number of hours of daylight varies sinusoidal over a period of twelve months.
This means that our function must repeat itself every twelve months. If we use the unit of the horizontal axis as months, the period of our function is equal to 12.
The period of a sine function usually is 2π, therefore, to make it repeat every 12 units, we need to divide this value by 12 and this will be our frequency.
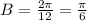
And finally, we need to find the phase. The sine function usually starts at the vertical translation value, and since the maximum point happens at x = 6, we want to translate the function 3 units to the right to have the minimum point at x = 0.
We do that by subtracting 3 from the argument
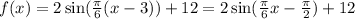
And this is the function that models our problem.
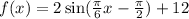
The graph of this function is
Where the y-axis represents the number of hours of daylight and the x-axis represents the corresponding month.