Step-by-step explanation:
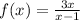
To find the domain we have to take a look at every part of the function that contains 'x'. In this function there are two places where x is:
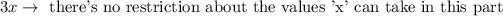
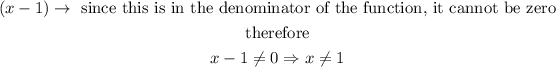
Answer:
The domain of the function is all real numbers except 1:

Around x = 1, the function goes to infinty. To the left of x = 1 it's negative infinity and to the right it's positive infinity