Question

Upon arrival at a hospital's emergency room, patients are categorized according to their condition as critical, serious, or stable. In the past year: • 12% of the emergency room patients were critical • 27% of the emergency room patients were serious the rest of the emergency room patients were stable • 43% of the critical patients died • 26% of the serious patients died and • 5% of the stable patients died. Find the probability that the patient who survived was categorized as serious upon arrival.

Answer 1

Let,

X1 = Patient that is Critical

X2 = Patient that is Serious

X3 = Patient that is Stable

D = Dead Patient

V = Survived Patient

Using Baye's Formula:

Let,

P(X2, V) = the probability that the patient who survived was categorized as serious upon arrival.​

`\text{ P (X}_i,V)\text{ = }\frac{P(X_i)\text{ x }P(X_i,V)}{P(X_1)\text{ x }P(X_1,V)\text{ + }P(X_2)\text{ x }P(X_2,V)\text{ + }\ldots\text{ +}P(X_n)\text{ x }P(X_n,V)}`

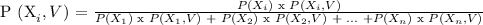
We are given,

P(X1) = 0.12

P(X2) = 0.27

P(X3) = 1 - (0.12 + 0.27) = 0.61

P(X1,V) = 1 - P(X1,D) = 1 - 0.43 = 0.57

P(X2,V) = 1 - P(X2,D) = 1 - 0.26 = 0.74

P(X3,V) = 1 - P(X3,D) = 1 - .05 = 0.95

We now solve for the probability that the patient who survived was categorized as serious upon arrival,

`P(X_2,V)\text{ = }\frac{(0.27)(0.74)}{(0.12)(0.57)\text{ + (0.27)(0.74) + (0.61)(0.95)}}\text{ =}(0.1998)/(0.8477)`
`P(X_2,V)\text{ = 0.2356965908 }\approx\text{ 0.}2357`

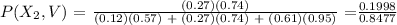
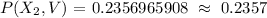
The probability that the patient who survived was categorized as serious upon arrival is 0.2357.