Question

Can you help me with the a, b and c!!!

Answer 1

The Richter magnitude of an earthquake is given by the following formula:

`R=0.67\log_{\placeholder{⬚}}(0.37E)+1.46`

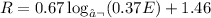
Where E is the energy (in kilowatt-hours) released by the earthquake.

a) What is the magnitude of an earthquake that releases 11,800,000,000 kw-h of energy?

We need to replace the E-value and solve for R:

`\begin{gathered} R=0.67\log_{\placeholder{⬚}}(0.37*11,800,000,000)+1.46 \\ R=0.67\log_{\placeholder{⬚}}(4,366,000,000)+1.46 \\ R=0.67*9.64+1.46 \\ R=6.46+1.46 \\ R=7.9 \end{gathered}`

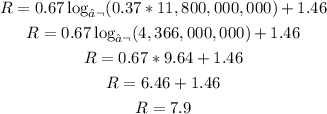
The magnitude of the earthquake is 7.9

b) How many kw-h of energy would an earthquake have to release in order to be an 8.2 on the Richter scale?

In this case we know the R-value, we replace it and solve for E:

`\begin{gathered} 8.2=0.67\log_{\placeholder{⬚}}(0.37E)+1.46 \\ 8.2-1.46=0.67\log_{\placeholder{⬚}}(0.37E) \\ 6.74=0.67\log_{\placeholder{⬚}}(0.37E) \\ (6.74)/(0.67)=log(0.37E) \\ 10.06=log(0.37E) \\ 10^(10.06)=10^(log(0.37E)) \\ 11473647221=0.37E \\ E=(11473647221)/(0.37) \\ E\approx31,009,857,353\text{ kw-h} \end{gathered}`

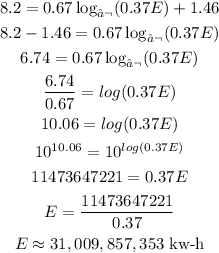
The earthquake has to release 31,009,857,353 kilowatt-hours in order to be an 8.2 on the Richter Scale.

c) What number of kw/h of energy would an earthquake have to release in order for walls to crack?

The problem says at a Richter magnitude of 4 and above, the walls in your house may start to crack. Then we need to replace R=4 and solve for E:

`\begin{gathered} 4=0.67log(0.37E)+1.46 \\ 4-1.46=0.67log(0.37E) \\ 2.54=0.67log(0.37E) \\ (2.54)/(0.67)=log(0.37E) \\ 3.79=log(0.37E) \\ 10^(3.79)=10^(log(0.37E)) \\ 6180.8=0.37E \\ E=(6180.8)/(0.37) \\ E=16704.9\text{ kw-h} \end{gathered}`

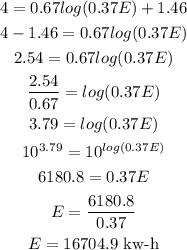
The earthquake has to release 16704.9 kilowatt-hours in order for walls to crack.