Question

HeyyThe sum of the first ten terms abeg1, 3/2, 7/4, 15/8, ...

Answer 1

First, recall the following formulas:

`\begin{gathered} \sum ^k_(n\mathop=1)c=ck \\ \\ \sum ^k_(n\mathop=1)r^(n-1)=(1-r^k)/(1-r) \end{gathered}`

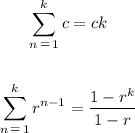
Next, find an expression for the n-th term of the given sequence. Notice that the given terms can be rewritten as follows:

`\begin{gathered} 1=2-1=2-(1)/(2^0) \\ (3)/(2)=2-(1)/(2)=2-(1)/(2^1) \\ (7)/(4)=2-(1)/(4)=2-(1)/(2^2) \\ (15)/(8)=2-(1)/(8)=2-(1)/(2^3) \end{gathered}`

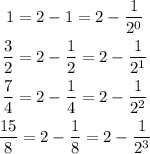
Then, the n-th term is given by the expression:

`a_n=2-(1)/(2^(n-1))`

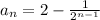
This expression accurately predicts the first four terms of the given sequence:

`\begin{gathered} a_1=2-(1)/(2^(1-1))=2-(1)/(2^0)=2-(1)/(1)=2-1=1 \\ a_2=2-(1)/(2^(2-1))=2-(1)/(2^1)=2-(1)/(2)=(4)/(2)-(1)/(2)=(3)/(2) \\ \ldots \end{gathered}`

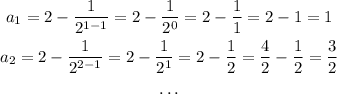
Then, the sum of the first ten terms is:

`\begin{gathered} \sum ^(10)_(n\mathop=1)a_n=\sum ^(10)_{n\mathop{=}1}(2-(1)/(2^(n-1))) \\ =\sum ^(10)_{n\mathop{=}1}2-\sum ^(10)_{n\mathop{=}1}(1)/(2^(n-1)) \\ =10\cdot2-\sum ^(10)_{n\mathop{=}1}(\frac{1}{2^{}})^(n-1) \\ =20-(1-((1)/(2))^(10))/(1-((1)/(2))) \\ =20-(1-(1)/(2^(10)))/(1-(1)/(2)) \\ =20-(((2^(10)-1)/(2^(10))))/(((1)/(2))) \\ =20-2((2^(10)-1)/(2^(10))) \\ =20-(2^(10)-1)/(2^9) \\ =20-(1024-1)/(512) \\ =20-(1023)/(512) \\ =(20\cdot512-1023)/(512) \\ =(10240-1023)/(512) \\ =(9217)/(512) \\ =18.001953125 \end{gathered}`

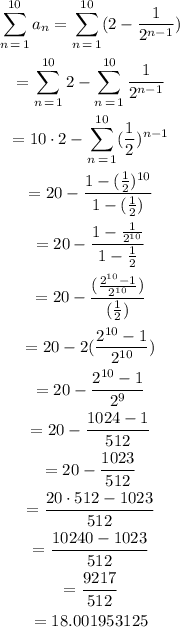
Therefore, the sum of the first ten terms of the sequence is equal to 9217/512, which in decimal notation is equal to 18.001953125.