Given:
The system of equations is,
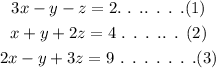
The objective is to solve the equations using the elimination method.
Step-by-step explanation:
Consider the equations (1) and (2).
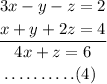
Now, consider the equations (2) and (3).
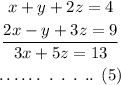
On multiplying the equation (4) with (-5),
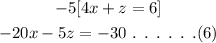
To find x :
On solving the equations (5) and (6),
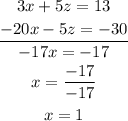
To find z :
Substitute the value of x in equation (6),
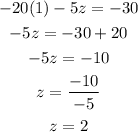
To find y :
Now, substitute the values of x and z in equation (2).
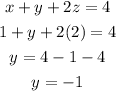
Hence, the value of x is 1, y is -1 and z is 2.