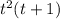Question

Identify whether each formula defines a rational function. If so, identify two polynomials whose ratio comprises it.

Answer 1

Given the function below

`k(t)=(4)/(t+1)-(3)/(t^2)`

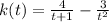
A rational function is a fraction where both numerator and denominator are polynomials, i.e

`\begin{gathered} k(t)=(4)/(t+1)-(3)/(t^2) \\ k(t)=(4t^2-3(t+1))/(t^2(t+1)) \\ k(t)=(4t^2-3t-3)/(t^2(t+1)) \end{gathered}`

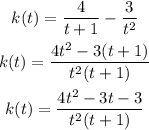
From the above deduction, both numerator and denominator are polynomials.

Hence, the given expression is a rational function.

The two polynomials whose ratio comprises the given rational function are

The numerator

`4t^2-3t-3`

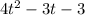
And the denominator

`t^2(t+1)`