Given
![y=3-\sqrt[]{3x-2}](https://img.qammunity.org/2023/formulas/mathematics/college/p7ay78uu03qnpmjyhpz0s89i9fwnsi5906.png)
We can analyse the range in parts, first, let's see the range of the square root function:
![y=\sqrt[]{3x-2}](https://img.qammunity.org/2023/formulas/mathematics/college/skb1cb4lreabszr9s3mg2awayaetlcg9u2.png)
A square root is always a positive number, because the square root of a negative number is not defined, so, the range of a square root is all positive numbers, including 0, here, it doesn't matter the function inside the square root, we just have to guarantee it's positive. So the range of the square root is
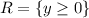
The graph is
As we can see, the range is all positive numbers, but if we put the minus sign, the range changes to all negative numbers, it's what happens here, because we have
![y=3-\sqrt[]{3x-2}](https://img.qammunity.org/2023/formulas/mathematics/college/p7ay78uu03qnpmjyhpz0s89i9fwnsi5906.png)
As we can see, the minus sign follows the square root, then the graph changes to
Now we are almost done. Now we just have to analyse how the constant +3 changes the range:
![y=3-\sqrt[]{3x-2}](https://img.qammunity.org/2023/formulas/mathematics/college/p7ay78uu03qnpmjyhpz0s89i9fwnsi5906.png)
Every time we sum a constant to a function we are moving the function up or down, if we do a sum, it's moving upwards, if it's subtraction, it's going downwards. Here, we have a sum, then we must move the graph 3 units up, then the final graph will be
Then, the range will change to all numbers below or equal 3.
Therefore, the final answer is
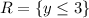
R = {y ≤ 3}