Question

A company is reviewing a batch of 26 products to determine if any are defective. On average, 3.6% of products are defective.What is the probability that the company will find 2 or fewer defective products in this batch?What is the probability that 4 or more defective products are found in this batch?If the company finds 5 defective products in this batch, should the company stop production?

Answer 1

The experiment has a binomial distribution just because the product could be or not defective. In this case you have n=26 the number of product that the company will check and you also know that the probability to get a defective one is 3.6%. Now we will proceed as follows, to find the probability of getting 2 or fewer defective products is exactly the same that

We also should notice that

`P(X=k)=(n;k)p^k(1-p)^((n-k));\text{ where }(n;k)=(n!)/(k!(n-k)!)`

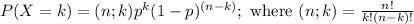
Now,

`P(X=0)=(26;0)(0.036)^0(1-0.036)^(26-0)=(1-0.036)^(26)\approx0.3855`
`P(X=1)=(26;1)(0.036)(1-0.036)^(26-1)=26(0.036)(1-0.036)^(25)\approx0.3743`
`P(X=2)=(26;2)(0.036)²(1-0.036)^(26-2)=325(0.001296)(1-0.036)^(24)\approx0.1747`

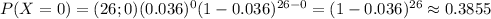
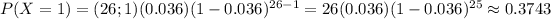
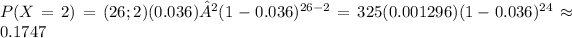
Then the probability that the company takes 2 or fewer defective products in this batch is

`P(X\leq2)=P(X=0)+P(X=1)+P(X=2)=0.3855+0.3743+0.1747=0.9345`

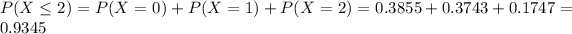
Now, to get the probability that the company find 4 or more defective products we proceed as follows. Since

`P(X\ge4)+P(X<4)=1,\text{ }`

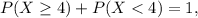
then

`P(X\ge4)=1-P(X<4)=1-(\text{ }P(X=0)+P(X=1)+P(X=2)+P(X=3)).`

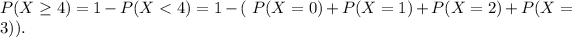
Notice that we only need to find one of these probabilities to get the answer.

`P(X=3)=(26;3)(0.036)³(1-0.036)^(26-3)=(23!(24)(25)(26))/(3!23!)(0.036)³(1-0.036)^(23)=0.05219`

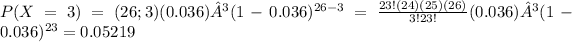
Then the probability to get more than 4 defective products is

`\begin{gathered} P(X\ge4)=1-(P(X=0)+P(X=1)+P(X=2)+P(X=3))= \\ =1-(0.9345+0.05219)=0.01331 \\ \\ P(X\ge4)=0.01331 \end{gathered}`

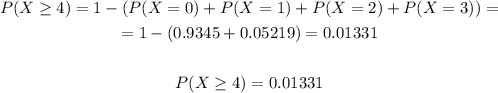
So if the company finds 5 defective products in this batch the company should stop the production because the probability to get more than 4 defective products is around 1.3%. It means that if you get 5 defective products even with this small probability then we could say that is really probable to get more defective products that those who were expected.