Question

Solve each equation by taking square roots. Give the answer in radical form, and then use a calculator to approximate the solution to two decimal places if necessary. A) (x+7)^2=64B) 5x^2+10=110

Answer 1

For part (a), using the square root property, take the square root of both sides of the equation. Thus, will eliminate the radical symbol on the left side of the equation.

`\begin{gathered} x+7=\pm\sqrt[]{64} \\ x+7=\pm8 \end{gathered}`

Note that the right side will either be positive or negative. This is because when we square both 8 and -8, we will obtain 64.

From the obtained equation, subtract 7 from both sides.

`x=\pm8-7`

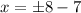
Thus, we will obtain two possible values of x.

`\begin{gathered} x=8-7=1 \\ \\ x=-8-7=-15 \end{gathered}`

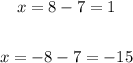
Therefore, for part (a), the value of x is -15 or 1.

For part (b), isolate the variable term by subtracting 10 from both side of the equation.

`\begin{gathered} 5x^2=110-10 \\ 5x^2=100 \end{gathered}`

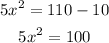
Divide both sides of the equation by 5.

`\begin{gathered} (5x^2)/(5)=(100)/(5) \\ x^2=20 \end{gathered}`

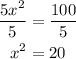
Similarly, take the square root of both sides of the equation by usng the square root property.

`\begin{gathered} x=\pm\sqrt[]{20} \\ x\approx\pm4.47 \end{gathered}`

Therefore, for part (b), the value of x is either approximately -4.47 or 4.47.