Question

The standard form for a parabola with vertex (h,k) and an axis of symmetry of y=k is:(y-k)^2=4p(x-h)The description below is for a parabola. Write it in standard form. When answering the questions type coordinates with parentheses and separated by a comma like this (x,y). If a value is a non-integer then type is a decimal rounded to the nearest hundredth.Vertex is (2,2); directrix is x=2-\sqrt[]{2}, focus is (2+\sqrt[]{2},2)The value for p is: AnswerThe value for h is: AnswerThe value for k is: Answer

Answer 1

Given that a parabola has

`\begin{gathered} Vertexis(2,2) \\ directrix\text{ }is\text{ }x=2-\sqrt[]{2} \\ focus\text{ }is\text{ }(2+\sqrt[]{2},2) \end{gathered}`

And that the standard form of a parabola can be expressed as

`\mleft(y-k\mright)^2=4p\mleft(x-h\mright)`

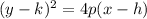
We are asked to find the value of p, h and k. This can be seen below.

Step-by-step explanation

Recall, If a parabola has a horizontal axis, the standard form of the equation of the parabola is this

`(y-k)^2=4p(x-h)`

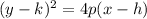
where p≠ 0. The vertex of this parabola is at (h, k). The focus is at (h + p, k). The directrix is the line x = h - p. The axis is the line y = k. If p > 0, the parabola opens to the right, and if p < 0, the parabola opens to the left.

Value of h and k

By comparison

`\begin{gathered} \text{Vetex = (h,k) = (2,2)} \\ \therefore h=2;k=2 \end{gathered}`

Answer: h = 2 and k =2

Value of p

Also, by comparison

`\begin{gathered} focus=(h+p,k)=(2+\sqrt[]{2},2) \\ \therefore p=\sqrt[]{2}=1.41 \\ \end{gathered}`

Answer : p =1.41

Writing the equation of the parabola in standard form

We can then use the given data to express the parabola in standard form as;

Answer

`(y-2)^2=4\sqrt[]{2}(x-2)`