Question

Use the transformation rule (x, y) - (x + 3, y + 1) to answer the following question.(Picture below)

Answer 1

`\begin{gathered} P(-2,3)\to P^(\prime)(1,4) \\ K(1,9)\to K^(\prime)(4,10) \\ R(5,6) \\ Yes \end{gathered}`

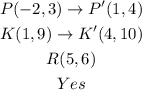
Step-by-step explanation

We want to apply the given rule to find the new points:

`(x,y)\to(x+3,y+1)`

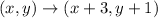
To do this, we have to add 3 to the x coordinate and 1 to the y coordinate of the preimage to get the image of the transformation (which is a translation).

Hence, for P(-2,3), the image is:

`\begin{gathered} P(-2,3)\to P^(\prime)^{}(-2+3,3+1) \\ P(-2,3)\to P^(\prime)(1,4) \end{gathered}`

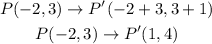
For K(1,9), the image is:

`\begin{gathered} K(1,9)\to K^(\prime)(1+3,9+1) \\ K(1,9)\to K^(\prime)(4,10) \end{gathered}`

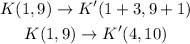
To find the preimage, we have to find the inverse of the transformation i.e. subtract 3 from the x coordinate and 1 from the y coordinate of the image.

Hence, the preimage of R is:

`\begin{gathered} R^(\prime)(8,7)\Rightarrow R(8-3,7-1) \\ \Rightarrow R(5,6) \end{gathered}`

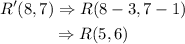
A transformation is an isometry when the shape preimage and the image of the transformation are congruent, in other words, they have the same shape and size.

The transformation above is a translation. A translation is an isometry because it moves the given shape through a fixed length in a fixed direction.

Hence, the transformation is an isometry.