Question

A genetic experiment with peas resulted in one sample of offspring that consisted of 475 green peas and 193 yellow peas. Find the 94% confidence interval to estimate the percentage of yellow peas. It was expected that 25% of the offspring peas would be yellow, do the results contradict the expectations? Round to the hundredths place of a percent-do not enter the % symbol.

Answer 1

Given:

Number of green peas = 475

Number of yellow peas = 193

Let's find the 94% confidence interval to estimate the percentage of yellow peas.

Where:

Total number of peas = 475 + 193 = 668

For the sample proportion, we have:

`\begin{gathered} p^(\prime)=(194)/(668) \\ \\ p^(\prime)=0.2889 \end{gathered}`

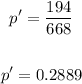
For a 94% confidence interval, the significance level will be:

1 - 0.94 = 0.06

For the critical value, using the z-table, we have:

`z_{(\alpha)/(2)}=z_{(0.06)/(2)}=z_(0.03)=1.881`

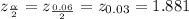
Now, to find the 94% confidence interval, apply the formula::

Where:

To find the margin of error E, we have:

`E=z_{(\alpha)/(a)}*\sqrt{(p^(\prime)(1-p^(\prime)))/(n)}=1.881*\sqrt{(0.2889(1-0.2889))/(668)}=0.032987`

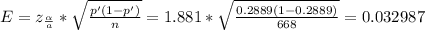
Thus, we have:

[tex]\begin{gathered} p^{\prime}-E

Hence the confidence interval will be:

Lower limit = 0.2559 ==> 25.59%

Upper limit = 0.3219 ==> 32.19 %

The confidence interval does not contain 0.25, hence we can say that the true results contradicts the expectations.

ANSWER:

The confidence interval does not contain the expectation of 25%, hence, the true results contradicts the expectation.