Question

14. What is the magnitude of the normal force acting on the block to the right the block is being pulled to the right by means of a rope and an angle of theta = 30° above the horizontal as shown the block weighs 20 N and the block ground interface is frictionless

Answer 1

Given,

The angle in which the force is applied, θ=30°

The weight of the block, W=20 N

The applied force, F_app=10.0 N

As the block is in vertical equilibrium, the net vertical force on the block is zero.

Therefore,

`\begin{gathered} N+F\sin \theta=W \\ \Rightarrow N=W-F\sin \theta \end{gathered}`

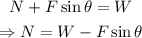
Where N is the normal force acting on the block.

On substituting the known values,

`\begin{gathered} N=20-10\sin 30\degree \\ =15\text{ N} \end{gathered}`

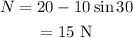
Thus the magnitude of the normal force acting on the block is 15 N