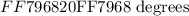Question

Find the measure of numbered angles for each triangle shown in the figure as ( 1 ).

Answer 1

The question pertains to the angle property of a triangle.

The angle property of a triangle states that:

" The sum of all interior angles in a triangle is always equal to 180 degrees "

We will apply the angle property of the triangle and find the required numbered ( 1 ) interior angle in each figure.

The first figure delineates a triangular shape of a mountain. Where two of the interior angles made between the slant heights of the mountain and the ground are given as follows:

`61\text{ degrees , 59 degrees }`

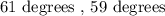
We will go ahead and express the angle property law of triangles in a mathematical form:

`\angle\textcolor{#FF7968}{1}\text{ + 61 + 59 = 180}`

We will go ahead and manipulate the above equation and determine the angle ( < 1 ) as follows:

`\begin{gathered} \angle1\text{ + 120 = 180 } \\ \angle1\text{ = 180 - 120} \\ \textcolor{#FF7968}{\angle1=}\text{\textcolor{#FF7968}{ 60 degrees}} \end{gathered}`

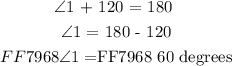
Hence, the required numbered interior angle for mountain figure is:

`\textcolor{#FF7968}{60}\text{\textcolor{#FF7968}{ degrees}}`

================================================================================

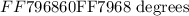
The next figure models the triangular shape of the roof of a house. The interior angle formed between the slant heights of the roof and the horizontal base of the roof , and the vertex of the triangle is given as follows:

`125\text{ degrees , 35 degrees}`

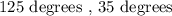
We will again apply the interior angle law for triangles which states:

`\angle1\text{ + 125 + 35 = 180}`

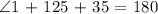
We will go ahead and manipulate the above equation and determine the angle ( < 1 ) as follows:

`\begin{gathered} \angle1\text{ + 160 = 180} \\ \angle1\text{ = 180 - 160} \\ \textcolor{#FF7968}{\angle1}\text{\textcolor{#FF7968}{ = 20 degrees}} \end{gathered}`

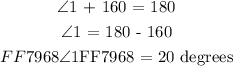
Hence, the required numbered interior angle for house roof figure is:

`\textcolor{#FF7968}{20}\text{\textcolor{#FF7968}{ degrees}}`