The Solution:
Given the diagram below:
Considering right-angled triangle ABC,
we can apply the Trigonometrical Ratio as below:
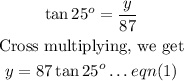
Similarly, considering right-angled triangle ABD,
we can apply the Trigonometrical Ratio as below:
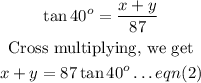
Now, putting eqn(1) into eqn(2), we get
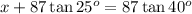
Solving for x, we have
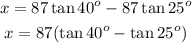
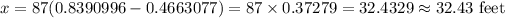
Therefore, the correct answer is 32.43 feet.