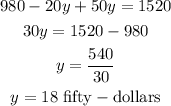Answer:
Explanation:
To solve this situation we can create a system of equations with the given information.
Let x be the number of twenties
Let y be the number of fifties.
If she has a total of $1,520:
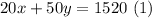
She has a total of 49 bills:
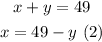
Then, substitute equation (2) into equation (1):
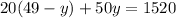
Solve for y.