Answer
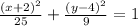
Explanation
In this case, the minor axis has the coordinates (-2, 1) and (-2, 7), then (referring to the above graph),
h = -2
Given that one focus is placed at (2, 4), then
k = 4
From the point (-2, 7) we can deduce that:
k+b = 7
4+b = 7
b = 7-4
b = 3
From the point (2, 4) we can deduce that:
h+c = 2
-2+c = 2
c = 2+2
c = 4
The relationship between the constants a, b, and c is:
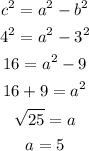
Equation of an ellipse
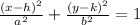
Substituting with the values previously found:
