Question

Can I Plss get some help on this can I get help on 48

Answer 1

To find the area of a kite, the formula is:

`A=(d_1d_2)/(2)`

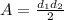
This means that we need to find the lengths of the diagonals. We can use the Pythagorean Theorem for this.

Let's first solve for the length of d1.

`\begin{gathered} x^2+x^2=11^2 \\ 2x^2=121 \\ x^2=(121)/(2) \\ x=(11√(2))/(2) \end{gathered}`

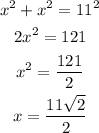
Because the d1 is twice the length of x, then

`d_1=2((11√(2))/(2))=11√(2)\approx15.6`

Now we solve for d2.

Again, we use the Pythagorean Theorem.

`((11√(2))/(2))^2+y^2=61^2`
`\begin{gathered} y^2=61^2-((11√(2))/(2))^2 \\ \\ y^2=(7,321)/(2) \\ \\ y\approx60.5 \end{gathered}`

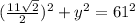
So d2 = 2y = 121.

To find the area, we multiply the diagonals then divide by 2.

`A=(15.6(121))/(2)=943.8`

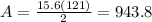
The area is approximately 943.8 square units.

The perimeter is much easier to find. We simply add all of the sides.

We know that a kite has 2 pairs of consecutive sides that are congruent.

So the perimeter is 11 + 11 + 61 + 61 or 144 units.