To find the area of a kite, the formula is:
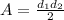
This means that we need to find the lengths of the diagonals. We can use the Pythagorean Theorem for this.
Let's first solve for the length of d1.
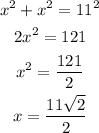
Because the d1 is twice the length of x, then
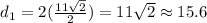
Now we solve for d2.
Again, we use the Pythagorean Theorem.
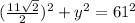
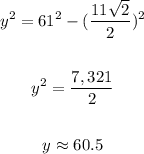
So d2 = 2y = 121.
To find the area, we multiply the diagonals then divide by 2.
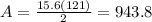
The area is approximately 943.8 square units.
The perimeter is much easier to find. We simply add all of the sides.
We know that a kite has 2 pairs of consecutive sides that are congruent.
So the perimeter is 11 + 11 + 61 + 61 or 144 units.