ANSWER

Step-by-step explanation
Parameters given:
Mass of smaller crate, m1 = 22 kg
Mass of larger crate, m2 = 92 kg
Coefficient of static friction between two crates, μs = 0.87
Coefficient of kinetic friction between two crates, μk = 0.68
1) The sum of forces acting in the horizontal direction on the smaller crate is:
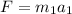
The sum of forces acting in the horizontal direction on the larger crate is:
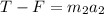
where F = frictional force, T = tension
To find the acceleration of the smaller crate, we have to substitute F from the first equation into the second equation:
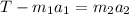
The acceleration is equal for both crates since the upper crate is static during the motion, which implies that:
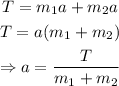
Substitute the given values:
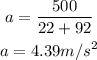
That is the acceleration of the smaller crate.
2) To find the frictional force on the smaller crate, substitute the value of acceleration, a, into the first equation:
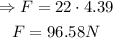
3) The maximum tension that the rope can be pulled at will occur when there is maximum friction.
That is:
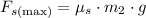
Applying the same principle from the first equation:
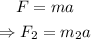
This implies that:
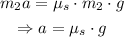
To find the tension, apply the already given formula:
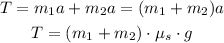
Therefore, the max tension is:
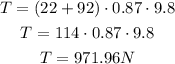
4) To find the acceleration of the smaller crate, we apply the formula for kinetic friction:
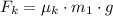
Recall that:
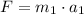
Therefore:

Substitute the given values:
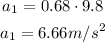
That is the acceleration of the smaller/upper crate.
5) Recall from the second equation that:
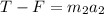
Substitute the formula for kinetic friction:
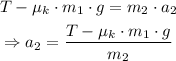
Substitute the given values to solve for a2:

That is the acceleration of the larger/lower crate.