The chef will end up with 300 mL of a dressing that is 9% vinegar. Let's calculate how much vinegar will the dressing have:
Therefore,
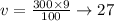
He'll have 27mL of vinegar.
Now, we know that x mL of the 5% dressing plus y mL of the 15% one will give the chef a total of 27mL of vinegar. Therefore,
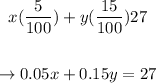
And that x mL of the 5% dressing plus y mL of the 15% one will give the chef a total of 300mL of dressing. Therefore,
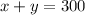
We have a system of equations:
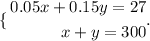
Let's clear y from equation 2 and replace in equation 1:
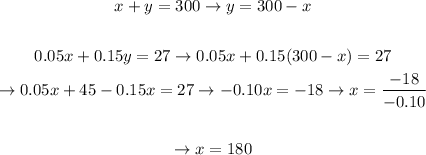
Thereby,
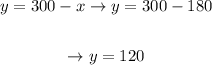
The chef would have to use 180mL of the dressing that's 5% vinegar, and 120mL of the one that's 15% vinegar.