We will investigate how to solve fractional equations involving variable ( x ).
The following equation is given:
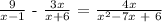
When dealing such fractional equations with variable in the denominator we try our best to remove the denominator or reduce the fractions to simpler expressions.
We will start by making factors of the quadratic expression in the denominator at the right hand side of the " = " sign:
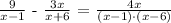
The factors for the above quadratic were ( -1 and -6 )!
Then we will take the LCM of the fractions on the left hand side of the " = " sign and form a common denominator as follows:
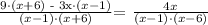
The LCM of the denominator was a product of induvidual denominators ( x - 1 ) & ( x + 6 )!
Now we will open the parenthesis for the numerator on the left hand side of the " = " sign and simultaneosuly cancel out the common denominator on both sides of the " = " sign i.e ( x - 1 )!
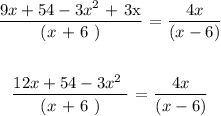
We will cross multiply across the " = " sign as follows:
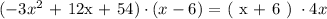
Then we will solve each parenthesis and group the common terms:

At the last step we moved all the terms to one side of the " = " sign. We are left with a cubic equation.
We will use a cubic equation solver to determine the roots of the cubic equation. The roots are:
![\begin{gathered} \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = }}\textcolor{#FF7968}{-2.5418} \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = }}\textcolor{#FF7968}{5.604}\text{\textcolor{#FF7968}{ }}\textcolor{#FF7968}{\pm}\text{\textcolor{#FF7968}{ }}\textcolor{#FF7968}{3.329}\text{\textcolor{#FF7968}{ ( conjugate pair )}} \end{gathered}]()