To answer this question we will set and solve a system of equations.
Let A be the speed (in miles per hour) of the airplane in still air, and W be the wind speed (in miles per hour).
Since the airplane flying with the wind takes 4 hours to travel a distance of 1200 miles and flying against the wind takes 5 hours to travel the same distance, then we can set the following equation:
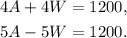
Dividing the first equation by 4 we get:
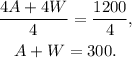
Subtracting A from the above equation we get:

Substituting the above equation in the second one we get:

Simplifying the above result we get:
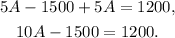
Adding 1500 to the above equation we get:
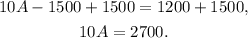
Dividing the above equation by 10 we get:
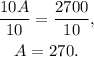
Finally, substituting A=270 at W=300-A we get:
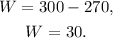
Answer:
The speed of the airplane in still air is 270 miles per hour.
The wind speed is 30 miles per hour.