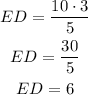Question

"When finding all the unknown values in similar right triangles you have choices: you can useproportional relationships or the Pythagorean Theorem. Which would you use for each of theseexamples, and why?"

Answer 1

We know that triangles ABC and DEF are similar. So, in order to find all the unknown values we can use proportional relationships because we have all values of the small triangle and at least, one value of the big triangle.

For instance, if we want to know the lenght of segment FD, the following ratio must be preserved:

`(BC)/(AC)=(FE)/(FD)`

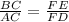
since BC=5 , AC=4 and EF=10, we have

`(5)/(4)=(10)/(FD)`

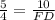
so ED is equal to

`\begin{gathered} FD=(4\cdot10)/(5) \\ FD=(40)/(5) \\ FD=8 \end{gathered}`

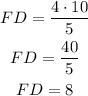
Similarly, we can obtain ED as

`(ED)/(10)=(3)/(5)`

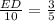
so, ED is

`\begin{gathered} ED=(10\cdot3)/(5) \\ ED=(30)/(5) \\ ED=6 \end{gathered}`