Question

What is the equation of the line tangent to the function f(x) = 2x² + 3x at the point (-2,2) ?

Answer 1

Answer:
`y\text{ = -5x - 8 \lparen option A\rparen}`

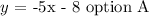
Step-by-step explanation:

Given:

f(x) = 2x² + 3x

Point: (-2, 2)

To find:

the equation of the line tangent to the function at point (-2, 2)

First we need to find the derivative of the given function:

`\begin{gathered} f^(\prime)(x)\text{ = 2\lparen2\rparen x}^(2-1)\text{ + 3} \\ f^(\prime)(x)\text{ = 4x + 3} \\ The\text{ derivative is the same as m = slope} \\ m\text{ = 4x + 3} \end{gathered}`

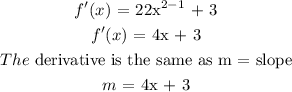
We need to get the value of m at point (-2, 2):

`\begin{gathered} from\text{ the point, x = -2} \\ substitute\text{ for x in the derivative} \\ m\text{ = 4\lparen-2\rparen + 3 = -8 + 3} \\ m\text{ = -5} \\ \end{gathered}`

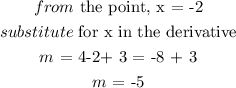
To get the equation of the line tangent to the function, we will use the formula:

`$$y-y_1=m(x-x_1)$$`
`\begin{gathered} x_1\text{ = -2, y}_1\text{ = 2} \\ y\text{ - 2 = -5\lparen x - \lparen-2\rparen\rparen} \\ y\text{ - 2 = -5\lparen x + 2\rparen} \\ y\text{ - 2 = -5x -10} \\ y\text{ = -5x -10 + 2} \\ y\text{ = -5x - 8 \lparen equation of the line tangent to the function\rparen} \\ \\ y\text{ = -5x - 8 \lparen option A\rparen} \end{gathered}`