Let the event D be that a person has the disease.
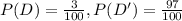
Now Let T be positive test and T' be a negative test result.
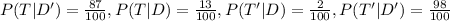
So the probability that the person has the disease given that the test is positive is given by:

So only 0.46% of the people who tested positive will have the disease.