Answer:
a) The Median stays the same
b) The Mean decreases by $27
Step-by-step explanation:
We were given the following weekly salaries:
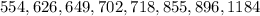
The mean & median for the data above is shown below:

Suppose that the $1184 salary changes to $968, we have:

Therefore,
a) The Median stays the same
b) The Mean decreases by $27