Question

Which of the following points lies on the given line?

Answer 1

To be able to identify which of the following points lies on the given lines, let's determine first the equation of the line and by using the given two points of the line to determine its slope (m) and its y-intercept (b).

Given two points: (0,-13.5) and (9,0)

Let's now determine the slope (m),

`\text{ m = }(y_2-y_1)/(x_2-x_2)\text{ = }\frac{0\text{ - (-13.5)}}{9\text{ - 0}}\text{ = }(13.5)/(9)`
`m\text{ = }(13.5)/(9)\text{ = }((13.5)/(4.5))/((9)/(4.5))\text{ = }(3)/(2)\text{ ; m = }(3)/(2)`

Let's determine the y-intercept by substituting m = 3/2 and x,y = 9,0 at the slope-intercept formula:

`\text{ y = mx + b }\rightarrow\text{ 0 = (}(3)/(2))(9)\text{ + b}`
`\text{ b + }(27)/(2)\text{ = 0 }\rightarrow\text{ b = -}(27)/(2)`

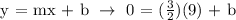
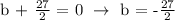
The equation of the line is, therefore,

`\text{ y = mx + b }\rightarrow\text{ y = (}(3)/(2))x\text{ - }(27)/(2)`
`\text{ y = }(3)/(2)x\text{ - }(27)/(2)\text{ }\rightarrow\text{ y = }(1)/(2)(3x\text{ - 27) }\rightarrow\text{ 2y = 3x - 27}`

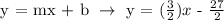
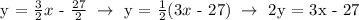
Using the equation of the line 2y = 3x - 27, let's plug in the points in the given choices. The point that will satisfy the equation is the point that lies on the given line.

a.) (10,2)

`2y\text{ = 3x - 27 }\rightarrow\text{ 2(2) = 3(10) - 27 }\rightarrow\text{ 4 = 30 - 27 }\rightarrow\text{ 4 }\\e\text{ 3}`

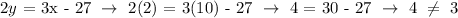
The point does not lie on the given line.

b.) (-1, -16)

`\text{ 2y = }3x\text{ - 27 }\rightarrow\text{ 2(-16) = 3(-1) - 27 }\rightarrow\text{ -32 = -3 - 27 }\rightarrow\text{ -32 }\\e\text{ -30}`

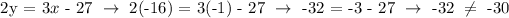
The point does not lie on the given line.

c.) (17,12)

`\text{ 2y = 3x -27 }\rightarrow\text{ 2(12) = 3(17) - 27 }\rightarrow\text{ 24 = 51 - 27 }\rightarrow\text{ 24 = 24}`

The point does lie on the given line.

d.) (-8,-25 1/4)

`2y\text{ = 3x - 27 }\rightarrow\text{ 2(-25}(1)/(4))\text{ = 2(-8) - 27 }\rightarrow\text{ 2(-}(101)/(4))\text{ = -16 - 27}`
`\text{ }\rightarrow\text{ -}(202)/(4)\text{ = -43 }\rightarrow\text{ -50.5 }\\e\text{ -43}`

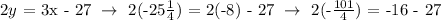
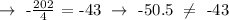
The point does not lie on the given line.

Therefore, only point (17,12) lines on the given line. The answer is C.