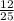Sample space (N(S)) = 50
Let A be the event of getting a number divisible by 3
A = {3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,48}
N(A) = 16
Therefore, the probability of a number divisible by 3 is
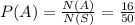
Let B be the event of getting a number divisible by 4
B = { 4,8,12,16,20,24,28,32,36,40,44,48}
N(B) = 12
Therefore, the probability of a number divisible by 4 is
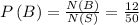
Also, the intersection between A and B is
A n B = { 12,24,36,48}
Therefore,
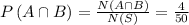
Hence, the probability that a number selected at random from the first 50 positive integers is exactly divisible by 3 or 4 will be
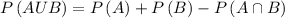
Therefore,
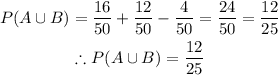
Hence, the answer is