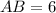Question

Circles P and O with a common external tangent Segment AB. OA=8PB=2Find AB:

Answer 1

We are given the common tangent of two circles. To determine the value of AB we need to form a right triangle and apply the Pythagorean theorem. The triangle will be formed by segment OP as the hypotenuse and the segment from O to the point where the perpendicular line to OA that passes through P as one of its sides. The length of this side is:

`\begin{gathered} b=OA-PB \\ b=8-2=6 \end{gathered}`

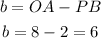
The value of segment OP is:

`OP=8+2=10`

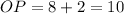
Applying the theorem:

`h=\sqrt[]{OP^2-b^2}`

Replacing the values:

`\begin{gathered} h=\sqrt[]{10^2-8^2} \\ h=\sqrt[]{100-64} \\ h=\sqrt[]{36} \\ h=6 \end{gathered}`

Since this segment has the same length as AB we have:

`AB=6`