Question

Find outside surface area and volume of the solid object assume that the base is regular

Answer 1

The solid object shown is the frustum of a square based pyramid..

To calculate the total surface area, we shall follow the procedure below;

`\begin{gathered} \text{Total Surface Area}=TSA \\ \text{TSA}=\lbrack(1)/(2)(P_1+P_2)L\rbrack+B_1+B_2 \\ \text{Where the variables are;} \\ P_1=Perimeter\text{ of base 1} \\ P_2=\text{Perimeter of base 2} \\ L=Slant\text{ height} \\ B_1=\text{Area of base 1} \\ B_2=\text{Area of base 2} \end{gathered}`

We shall now solve as follows;

`\begin{gathered} P_1=2(l+w) \\ P_1=2(14+14) \\ P_1=2(28) \\ P_1=56in \end{gathered}`
`\begin{gathered} P_2=2(l+w) \\ P_2=2(24+24) \\ P_2=2(48) \\ P_2=96in \end{gathered}`
`\begin{gathered} B_1=l* w \\ B_1=14*14 \\ B_1=196in^2 \end{gathered}`
`\begin{gathered} B_2=l* w \\ B_2=24*24 \\ B_2=576in^2 \end{gathered}`

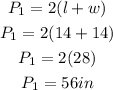
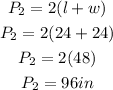
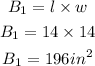
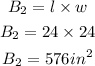
The total surface area would now be;

`\begin{gathered} \text{TSA}=\lbrack(1)/(2)(P_1+P_2)L\rbrack+B_1+B_2 \\ \text{TSA}=\lbrack(1)/(2)(56+96)19\rbrack+196+576 \\ \text{TSA}=\lbrack(1)/(2)(152)19\rbrack+772 \\ \text{TSA}=\lbrack76*19\rbrack+772 \\ \text{TSA}=1444+772 \\ \text{TSA}=2216in^2 \end{gathered}`

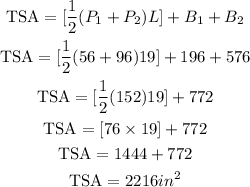
The volume of a frustum of a square based pyramid is given as;

`\begin{gathered} Vol=(1)/(3)h(B_1+B_2+\sqrt[]{B_1B_2}) \\ \text{Where;} \\ h=vertical\text{ height (altitude)} \end{gathered}`

The volume would now be;

`\begin{gathered} \text{Vol}=(1)/(3)*15(196+576+\sqrt[]{196*576}) \\ \text{Vol}=5(772+\sqrt[]{112896}) \\ \text{Vol}=5(772+336) \\ \text{Vol}=5(1108) \\ \text{Vol}=5540in^3 \end{gathered}`

ANSWER:

Therefore, we have

Total surface area = 2,216 inches squared

Volume = 5,540 inches cubed