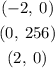Question

the graph of y=(x^2-4)^4(x^2+1)^ 5 is shown to the right. Find the coordinates of the local maximum points and minimum points

Answer 1

Step 1

Given;

`y=(x^2-4)^4(x^2+1)^5`

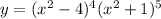
Required; To find the coordinates of the local minima and maxima

Step 2

Find the local minima and maxima

`\begin{gathered} \mathrm{Suppose\:that\:}x=c\mathrm{\:is\:a\:critical\:point\:of\:}f\left(x\right)\mathrm{\:then,\:} \\ \mathrm{If\:}f\:'\left(x\right)>0\mathrm{\:to\:the\:left\:of\:}x=c\mathrm{\:and\:}f\:'\left(x\right)<0\mathrm{\:to\:the\:right\:of\:}x=c\mathrm{\:then\:}x=c\mathrm{\:is\:a\:local\:maximum.} \\ \mathrm{If\:}f\:'\left(x\right)<0\mathrm{\:to\:the\:left\:of\:}x=c\mathrm{\:and\:}f\:'\left(x\right)>\:0\mathrm{\:to\:the\:right\:of\:}x=c\mathrm{\:then\:}x=c\mathrm{\:is\:a\:local\:minimum.} \\ \mathrm{If\:}f\:'\left(x\right)\mathrm{\:is\:the\:same\:sign\:on\:both\:sides\:of\:}x=c\mathrm{\:then\:}x=c \\ \mathrm{\:is\:neither\:a\:local\:maximum\:nor\:a\:local\:minimum.} \end{gathered}`

Therefore; f'(x) is given as;

`f^(\prime)(x)=2x(x^2-4)^3(x^2+1)^4[9x^2-16]`

Step 3

Find the increasing and decreasing intervals from the graph

Plugin -4/3 into y

`\mathrm{Maximum}\left(-(4)/(3),\:(5^(14)\cdot \:256)/(387420489)\right)`

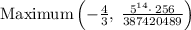
Plugin x=0 into y

`\mathrm{Minimum}\left(0,\:256\right)`

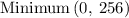
Plugin x=4/3

`\mathrm{Maximum}\left((4)/(3),\:(5^(14)\cdot \:256)/(387420489)\right)`

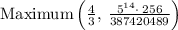
Plugging x=2 into y

`\mathrm{Minimum}\left(2,\:0\right)`

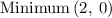
Answer; The maximum points are;

`\begin{gathered} ((4)/(3),(5^(14)*256)/(387420489))\text{ or \lparen1.33},4033.09) \\ \left(-(4)/(3),\:(5^(14)\cdot\:256)/(387420489)\right)or\text{ \lparen-1.33},\text{ 4033.09\rparen} \end{gathered}`

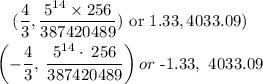
The minimum points are ;

`\begin{gathered} \left(-2,\:0\right) \\ \left(0,\:256\right) \\ \left(2,\:0\right) \end{gathered}`