Question

The bob of a pendulum travels a distance of 15 in. on the first swing after it is released. On each successive swing, the bob travels 85% of the previous distance.Write the explicit formula for the geometric sequence whose terms represent the distance traveled by the bob on each successive swing.

Answer 1

We have to write this model as a geometric sequence.

We know that the first term will have a value of 15, corresponding to the distance of the first swing.

Then, the second term will be 0.85 (or 85%) of the first term. This gives us the ratio of the geometric sequence:

`r=(a_2)/(a_1)=0.85`

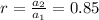
Then, we can find the explicit formula as:

`\begin{gathered} a_1=15 \\ a_2=r\cdot a_1=0.85\cdot15 \\ a_3=r\cdot a_2=r^2\cdot a_1=(0.85)^2\cdot15 \\ a_n=r\cdot a_(n-1)=r^(n-1)\cdot a_1=(0.85)^(n-1)\cdot15 \\ a_n=15\cdot(0.85)^(n-1) \end{gathered}`

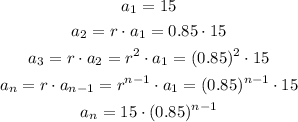
Answer: an = 15*(0.85)^(n-1) [Option B]