Given:
• Mass of first car 1, m1 = 1750 kg
,
• Mass of second car, m2 = 700 kg
,
• Initial velocity of car 1, u1 = 6.00 m/s due south
,
• Initial velocity of car 2, u2 = 19.0 m/s due west.
Let's solve for the following:
• (a). Calculate the final velocity of the cars.
Apply the conservation of momentum.
In the West direction(x-direction), we have:
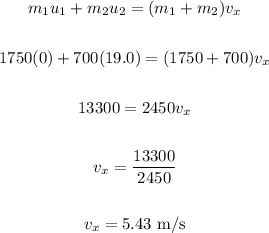
In the South direction (y-direction), we have:
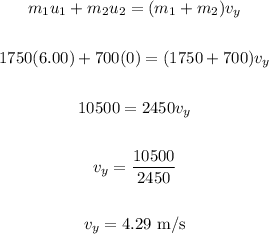
To find the magnitude, we have:
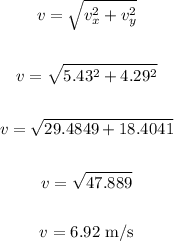
To find the direction, apply the formula:
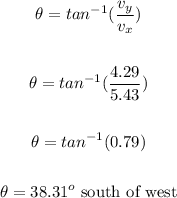
• (b). How much kinetic energy is lost in the collision?
To find the loss of kinetic energy, apply the formula:
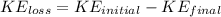
Using the Kinetic energy formula, we have:
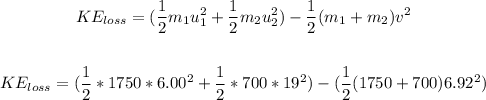
Solving further:
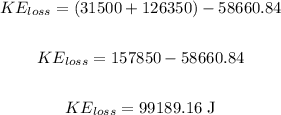
Therefore, the amount of kinetic energy lost is 99189.16 J.
• ANSWER:
(a). Magnitude = 6.92 m/s
Direction = 38.31° South of West
(b). 99189.16 J.