Question

If $40,000 is invested in an account at 6.5% interest rate compounded continuously. How much money will be in the account after 21 years?(Round to the nearest hundredth)

Answer 1

Step-by-step explanation:

$40,000 Is invested in an account, which gives a 6.5% rate compounded continuously, assuming that the compounding frequency is yearly, we have to find the amount after 21 years.

The answer can be found using the following formula for compound interest:

`A=P(1+(r)/(n))^(nt)\rightarrow(1)`

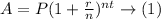
Plugging in the known variable values in equation (1) we can calculate the unknown final amount A, the steps are shown below:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ \\ r=(6.5)/(100)=0.065 \\ r=0.065 \\ n=1 \\ t=21 \\ P=\$40,000 \\ \\ \therefore\rightarrow \\ \\ A=(40,000)(1+(0.065)/(1))^((1*21)) \\ A=(40,000)(1.065)^((1*21)) \\ A=150,107.279 \\ \\ A\approx\$150,107.28 \end{gathered}`

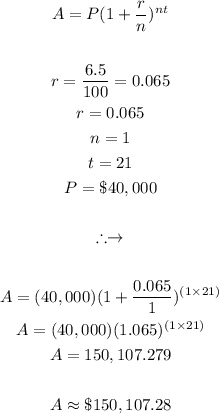
Therefore after 21 years, the money in the account would be $150,107.28.