Question

A positive B negative C zeroD the parabola opens upE the parabola opens up F the parabola opens down

Answer 1

Step 1:

The general parabolic function is given as:

`\text{y = ax}^2+bx+c`

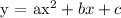
If a is positive, the parabola is upward.

If a is negative, the parabola is downward.

Step 2

The c-value is where the graph intersects the y-axis. In this graph, the c-value is -3. The graph of a parabola that opens up looks like this. The c-value is where the graph intersects the y-axis.

Step 3:

Finally, the c-value can also be called the y-intercept of the parabola. Algebraically, this is where the x-value is zero and graphically, this is where the graph intersects the y-axis.

Final answer

The c value of the function represented in the graph is -3 because the parabola opens up.