We have the next inequality:
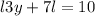
Apply the absolute value properties:
![\text{lal}=0\text{ so }-a<u>Which means :[tex]-10<3y+7<10](https://img.qammunity.org/2023/formulas/mathematics/college/fy4jpr0ksmfyr4x6x6l7funatksxxugzc0.png)
3y+7>-10 and 3y+7<10
Solve the inequalities:
for 3y+7>-10
3y>-10-7
y>-17/3
Now, for 3y+7<10
3y<10-7
3y< 3
y< 3/3
y< 1
So the solution is -17/3 < y < 1
Interval notation (-17/3, 1)
Now, the graph:
x can take any real value
y has the interval (-17/3, 1)
-17/3 = -5.6
on y -axis -5.6 and 1 are asymptotes.