Question

This table represents a quadratic function with a vertex at (1, 2). What is theaverage rate of change for the interval from x = 5 to x = 6?ху122336411518A. 27B. 18C. 9D. 3

Answer 1

Let's first determine the quadratic formula:

In vertex form:

Given,

Vertex = (h, k) = (1, 2)

The quadratic equation in vertex form: y = f(x) = a(x - h)² + k

Plugging in the vertex (1, 2):

f(x) = a(x - h)² + k

f(x) = a(x - 1)² + 2

Let's use the data in the given table to find a. Let's use (5, 18)

f(x) = a(x - 1)² + 2

18 = a(5 - 1)² + 2

18 = a(4)² + 2

18 = a(16) + 2

18 - 2 = 16a

16 = 16a

16/16 = 16a/16

1 = a

Thus, a = 1

The quadratic equation that represents the given table is, therefore:

f(x) = a(x - 1)² + 2

f(x) = 1(x - 1)² + 2

f(x) = (x - 1)² + 2

Since we now have the quadratic equation, let's determine the y-value at x = 6.

x = 6

f(6) = (x - 1)² + 2

= (6 - 1)² + 2

= (5)² + 2

= 25 + 2

f(6) = 27

Recall:

x = 5 ; y = f(5) = 18

x = 6 : y = f(6) = 27

Let's now determine the rate of change from x = 5 to x = 6.

`\text{ Rate of change = }\frac{f(6)\text{ - f(5)}}{x_6-x_5}\text{ = }\frac{27\text{ - 18}}{6\text{ - 5}}`
`\text{ = }\frac{9\text{ }}{1}`
`\text{ Rate of change = 9}`

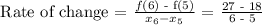
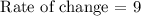
Therefore, the rate of change from x = 5 to x = 6 is 9.

The answer is letter C.