SOLUTION:
Case: Angle of Arc of a circle
An arc measure is an angle the arc makes at the center of a circle, whereas the arc length is the span along the arc. This angle measure can be in radians or degrees.
This is described in the image below:
Given: The angle subtended by the major and minor arcs
Required: To find:
A) the value of x
B) angle ABC
Method:
A) The value of x
The sum of the angles subtended by the minor and major arcs is 360 degrees
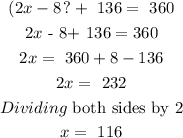
B) the angle subtended by arc ABC
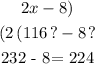
Final answer:
A) x= 116 degrees
B) angle ACD = 224 degrees