Question

find the value of x and find m angle ACD Do not write any units in your answer. Label the measure of (the yellow) arc ABC = (2x - 8)o.

Answer 1

Case: Angle of Arc of a circle

An arc measure is an angle the arc makes at the center of a circle, whereas the arc length is the span along the arc. This angle measure can be in radians or degrees.

This is described in the image below:

Given: The angle subtended by the major and minor arcs

Required: To find:

A) the value of x

B) angle ABC

Method:

A) The value of x

The sum of the angles subtended by the minor and major arcs is 360 degrees

`\begin{gathered} \left(2x-8\right?\degree+\text{ 136}\degree=\text{ 360}\degree \\ 2x\text{ - 8}\degree\text{+ 136}\degree=360\degree \\ 2x=\text{ 360}\degree+8\degree-136\degree \\ 2x=\text{ 232}\degree \\ Dividing\text{ both sides by 2} \\ x=\text{ 116}\degree \end{gathered}`

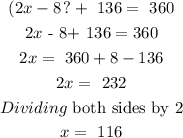
B) the angle subtended by arc ABC

`\begin{gathered} \lparen2x-8) \\ \left(2\left(116\right?-8\right? \\ 232\text{ - 8= 224}\degree \end{gathered}`

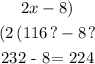
Final answer:

A) x= 116 degrees

B) angle ACD = 224 degrees