Question

A skier (with the weight of 920 N) has climbed a 6.0 m high hill and will ski down. He started down the hill with an initial velocity of 2.2 m/s. Being a klutz, he made it down the hill but hit a snow bank at the very bottom. Assume no friction and calculate: a) the skier’s velocity at the bottom of the hill as he impacts and b) the average force the snowdrift puts on him if he came to a complete stop in 90 cm

Answer 1

a)

We know that the potential energy is given by:

`U=Wh`

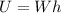
and the kinetic energy is:

`K=(1)/(2)mv^2`

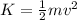
the mass of the skier is given by:

`m=(W)/(g)`

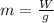
The total mechanical energy is the sum of the potential and kinetic energy; at the hill we know that:

• The velocity is 2.2 m/s.

,

• The height is 6 m

Plugging these values and the weight and mass we mentioned before we have that the mechanical energy at the hill is:

`(920)(6)+(1)/(2)((920)/(9.8))(2.2)^2=5747.18`

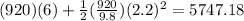
We know that the energy is conserved which means that at any given point the energy is the same; for this reason we know that the energy at the bottom is 5747.18 J. At this point the potential energy is zero which means that all the energy is kinetic, then we have:

`\begin{gathered} (1)/(2)((920)/(9.8))v^2=5747.18 \\ v^2=((2)(9.8)(5747.18))/(920) \\ v^=\sqrt{((2)(9.8)(5747.18))/(920)} \\ v=11.07 \end{gathered}`

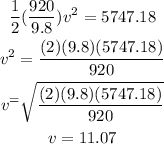
Therefore, the velocity at the bottom of the hill is 11.07 m/s.

b)

To obtain the average force we need to find the work first. By the work energy theorem which states that:

`W=K_f-K_0`

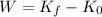
then we have:

`\begin{gathered} W=5747.18-(1)/(2)((920)/(9.8))(2.2)^2 \\ W=5520 \end{gathered}`

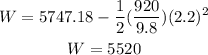
Hence the snowdrifts do 5520 J on the skier.

Now we just need to remember that:

`W=Fd`

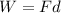
Then:

`\begin{gathered} 5520=0.9d \\ d=(5520)/(0.9) \\ d=6133.33 \end{gathered}`

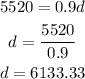
Therefore, the average force is 6133.33 N