Question

Step 1 of 2: Reduce the rational expression to lowest terms x/x^2 - 4xStep 2 of 2: Find the restricted values of X, if any, for the given rational expression.

Answer 1

We have the following expression:

`(x)/(x^2-4x)`

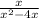
Step 1. Reduce the rational expression to the lowest tem

By factoring the variable x, we get

`(x)/(x(x-4))`

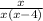
We can cancel x out as long as x is different from zero. Then one restricted value is x=0. So, If x is different from zero, our expression can be reduced to

`(x)/(x^2-4x)=(1)/(x-4)`

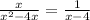
but x must be different from 4.

Step 2. Find the restricted values of x.

Since x can not be zero or four, the restricted values are x=0 and x=4