We have the following expression:
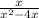
Step 1. Reduce the rational expression to the lowest tem
By factoring the variable x, we get
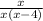
We can cancel x out as long as x is different from zero. Then one restricted value is x=0. So, If x is different from zero, our expression can be reduced to
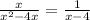
but x must be different from 4.
Step 2. Find the restricted values of x.
Since x can not be zero or four, the restricted values are x=0 and x=4